A formula that can be used for calculating compound interest
A = P( 1 + (r/n) )^nt ; R = r * 100 Where: A= Total Accrued Amount (Principal + Interest) P = Principal Amount R = Rate of Interest per year as a decimal ; r = R/100 so 4% is 4 and r would be 0.04 t = number of periods n = compounding period (^ indicates to the power of) Note: Remember BODMAS when calculating with variables
Reasoning – this breaks interest down into individual compounding periods. For example, within a year when dealing with months, r would be divided by 12 if the source of interest is annual based. The individual periods are then compounded using the power over all the periods eg 24 periods for 2 years – see the examples below. NOTE the r/n is an empirical adjustment required because quoted interest rates from most sources are over a year (annual). Whenever obtaining interest rates from a source we must be careful with the r/n calculation as it may need to be ignored. If for some reason the period over which interest is defined in the source list is anything other than annually this r/n calculation may require alteration..
UK Base Interest Rates source
Bank of England Base Rate
XLS File of Base Rate changes since 1664 to June 2022
Note – I took a snap shot at June 2022 for latest go to Bank of England base rate where there is(at October 2022) a constantly updated xls file.
So for example if we want to calculate interest on £100,000 over a period of 4 years and 8 months based on an interest rate of 4.0% over the base of 0.5% over differing compound periods;
Compounded annually;
A = 100,000 ( 1 + (0.045/1) )^4.67 = £122,821.10
A = £122,821.10
Compounded Monthly;
A = 100,000 ( 1 + (0.045/12) )^56 = £123,319.40
A = £123,319.40
Compounded Daily
A = 100,000 ( 1 + (0.045/365) )^1704 = 123,376.30
A = £123,376.30
Please note : simplification this calculation leap years re-calculate if important
(^ indicates to the power of)
Methodology – How to calculate the Interest rate to be used
At the Bank of England the Monetary Policy Committee (MPC) made up of appointed members set the bank of England Base rate. When they do this it normally makes the national news. For example on the 3rd of August 2023 the Monetary Policy committee set the interest rate at 5.25%. This is the interest figure I use in the above compound interest rate when I need to calculate interest to be added by the council for holding money over a given period. But because for any given period it is unlikely that interest rates will have been uniform for the entire period it is necessary to either calculate one figure for the entire period or alternatively calculate the interest on the principle for each sub period and aggregate the figure for each of the periods. Below shows a method of calculating a single average daily interest rate for any period given changes to the rates.
So for example:
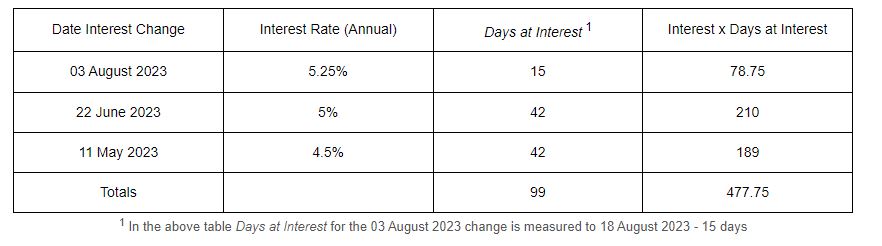
Calculate the interest rate to be used for a return of developer contributions received on the 11 May 2023 and required to be returned on the 18 August 2023 in the knowledge that the interest rate on the 11 May 2023 was 4.5% but was raised by the MPC to 5% on 22 June 2023 and then raised to 5.25% on the 03 August 2023. Develop a framework that can be used to calculate an applicable interest rate that can be used in the compounding interest rate calculation.
Average interest rate over this period is calculated as 477.75/99 or 4.825757%
This figure is consistent with the reporting by the Bank of England which changes rates on individual days rather than at the end of years or months. As such we should use the Compounding on a Daily basis to calculate the compounded interest to be returned as a result of holding this money for 99 days.
Normally, for developer contributions, additional interest will be calculated over periods of years rather than mere days but the above template can be used for any given time period. Additionally and importantly it calculates the total number of days which is also required for the compound interest rate calculation.