Category: Applied Mathematics

Methodology Compound Interest Calculation (Updated October 2023)

A formula that can be used for calculating compound interest

A = P( 1 + (r/n) )^nt ; R = r * 100

Where:
A= Total Accrued Amount (Principal + Interest)
P = Principal Amount
R = Rate of Interest per year as a decimal 
; r = R/100 so 4% is 4 and r would be 0.04
t = number of periods
n = compounding period
(^ indicates to the power of)

Note: Remember BODMAS when calculating with variables

Reasoning – this breaks interest down into individual compounding periods. For example, within a year when dealing with months, r would be divided by 12 if the source of interest is annual based. The individual periods are then compounded using the power over all the periods eg 24 periods for 2 years – see the examples below. NOTE the r/n is an empirical adjustment required because quoted interest rates from most sources are over a year (annual). Whenever obtaining interest rates from a source we must be careful with the r/n calculation as it may need to be ignored. If for some reason the period over which interest is defined in the source list is anything other than annually this r/n calculation may require alteration..

UK Base Interest Rates source
Bank of England Base Rate

XLS File of Base Rate changes since 1664 to June 2022
Note – I took a snap shot at June 2022 for latest go to Bank of England base rate where there is(at October 2022) a constantly updated xls file.

So for example if we want to calculate interest on £100,000 over a period of 4 years and 8 months based on an interest rate of 4.0% over the base of 0.5% over differing compound periods;
Compounded annually;
A = 100,000 ( 1 + (0.045/1) )^4.67 = £122,821.10
A = £122,821.10

Compounded Monthly;
A = 100,000 ( 1 + (0.045/12) )^56 = £123,319.40
A = £123,319.40

Compounded Daily
A = 100,000 ( 1 + (0.045/365) )^1704 = 123,376.30
A = £123,376.30
Please note : simplification this calculation leap years re-calculate if important
(^ indicates to the power of)

Methodology – How to calculate the Interest rate to be used

At the Bank of England the Monetary Policy Committee (MPC) made up of appointed members set the bank of England Base rate. When they do this it normally makes the national news. For example on the 3rd of August 2023 the Monetary Policy committee set the interest rate at 5.25%. This is the interest figure I use in the above compound interest rate when I need to calculate interest to be added by the council for holding money over a given period. But because for any given period it is unlikely that interest rates will have been uniform for the entire period it is necessary to either calculate one figure for the entire period or alternatively calculate the interest on the principle for each sub period and aggregate the figure for each of the periods. Below shows a method of calculating a single average daily interest rate for any period given changes to the rates.

So for example:

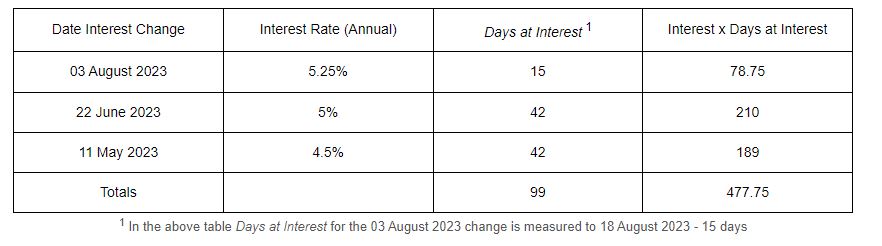
Calculate the interest rate to be used for a return of developer contributions received on the 11 May 2023 and required to be returned on the 18 August 2023 in the knowledge that the interest rate on the 11 May 2023 was 4.5% but was raised by the MPC to 5% on 22 June 2023 and then raised to 5.25% on the 03 August 2023. Develop a framework that can be used to calculate an applicable interest rate that can be used in the compounding interest rate calculation.

Average interest rate over this period is calculated as 477.75/99 or 4.825757%

This figure is consistent with the reporting by the Bank of England which changes rates on individual days rather than at the end of years or months. As such we should use the Compounding on a Daily basis to calculate the compounded interest to be returned as a result of holding this money for 99 days.

Normally, for developer contributions, additional interest will be calculated over periods of years rather than mere days but the above template can be used for any given time period. Additionally and importantly it calculates the total number of days which is also required for the compound interest rate calculation.

A detailed explanation of the Algebraic modeling using SQL for a Race Timing System

Running-a-Race
I know I’ve given an overview of what I did to create the timing system but here is the kernel explanation of the algebra modeled in SQL that does the real heavy lifting in my system and probably most other timing systems as well.

A review of the problem firstly;
The data works on the principle of a chip passing a matt. As the chip passes the matt times are recorded in a timing box which will then be passed through to a database.

Problem is that the timing matt will give multiple readings every time a runner runs across the matt and he or she may be running across multiple times the results only need the first of those passes and not any of the other reads as they are duplicates of a single pass.

If we take a simple example.
Imagine a race with two runners Runner 1 and Runner 2.

Runner 1 and Runner 2 start at the same time 01:00:00 by both passing a matt

Runner 1 finishes across the matt first at 01:30:00
Runner 2 finishes second at 01:35:00

The timing box picks up all following times
ID RFIDtag Time
1 Runner1 01:00:00
2 Runner1 01:00:07
10 Runner2 01:00:00
11 Runner2 01:00:05
15 Runner1 01:30:00
16 Runner1 01:30:10
17 Runner2 01:35:00
18 Runner2 01:35:01
19 Runner2 01:35:02

The first step would be to sort these by the Runner

So that we get
MyTable (sorted first by RFIDtag then by time.
RFIDtag Time
Runner1 01:00:00
Runner1 01:00:07
Runner1 01:30:00
Runner1 01:30:10
Runner2 01:00:00
Runner2 01:00:05
Runner2 01:35:00
Runner2 01:35:01
Runner2 01:35:0

We then need to somehow programmatically or via a query identify times that are relevant against times that are not relevant. So how is this done? Well the trick here is to algebraically model this in SQL using alias tables. You compare the table above against itself and only select for those times where the runner is the same. Here we use a 20 second window or gate and ID field is added back into MyTable (ID field MUST be automatically incremented and unique ie a primary key)

SELECT T1.*
FROM MyTable T1
WHERE EXISTS
(SELECT T2.*
 FROM MyTable T2
 WHERE T2.RFIDtag = T1.RFIDtag
 AND T2.ID   <  T1.ID
 AND T2.Time <= T1.Time
 AND T2.Time >= T1.Time - TimeSerial(0, 0, 20));

In my database application I create a variable for the 20 number which in this example equates to 20 seconds and I have made it easy to alter this period through a simple user interface. I call this period the GATE and it means that for a given race an appropriate gate can be set. In this way the application easily copes with lapped races.

A really beautiful and simple pattern which must be used very widely.

Keyser Söze, Code and the World Cup

world-cup-fifa_1401359010

It seems appropriate given the name of this site and 2014 being a world cup year that I might post something on code that I found a while back now related to establishing fixtures in a league coded by, for me, a mythical character. Back then I was taking part in a squash league with some friends and we needed to figure out some way of organising the matches for everyone. Seemed simple enough everyone plays everyone else on consecutive weekends. Turns out its not quite so easy and there’s a whole branch of mathematics called combinatronics that specifically looks at the way of optimising this kind of problem. In that really humble syntax of mathematicians I heard this phrase being banded about – a non trivial problem. As ever I turned to the internet and found some code by someone called Dev Ashish. Now I don’t know about you but prior to the internet I never had access to this kinds of expert and the power of the code really blew me away. The code very neatly creates the required number of matches in a table and allows me to organise matches for individuals to play each other and from there I was able to keep scores on everyone. It was in a word a bit of genius coding.

That was approximately 2005 and come 2014 and my blog the world cup reminded me of this amazing piece of coding.
I have my suspicions of where Dev Ashish is now but I can’t tell for sure.

Keyser Söze / Woland / Dev Ashish – they’re out there…

Joking aside many thanks to Dev Ashish for posting an amazing piece of code…

Option Compare Database
Option Explicit

Public intLeagueno As Integer
Public strLeaguenme As String


Function CalculateFixtures(ByVal Age As Integer, ByVal startdate As Date, ByVal EndDate As Date) As Integer

'**************************************************
' Set Database connections and Recordsets Variables
' Coded by Dev Ashish
'**************************************************
Dim cnn As ADODB.Connection
Dim rstTeams As ADODB.Recordset
Dim rstFixtures As ADODB.Recordset
    
'****************************************
' Create Integer Variables
'****************************************
Dim NumberofFixtures As Integer     ' Number of Fixtures between teams
Dim NumberofMatches As Integer      ' Number of Matches to be played
Dim NumberofTeams As Integer        ' Number of Teams
Dim Week As Integer                 ' Week Number for Fixtures

Dim FirstTeam As Integer
Dim LastTeam As Integer

Dim StartPosition As Integer

    Dim strtdate As String
    Dim intMsgbox As Integer
    strtdate = InputBox("Enter the date you want the league to start", "Question?")
    If (strtdate = "") Then
    intMsgbox = MsgBox("Thanks anyway")
    startdate = 3500
    
    Else
    startdate = strtdate
    intMsgbox = MsgBox("Calculating the fixtures starting" & " " & startdate, vbOKOnly, "Result")
    
End If

Dim iCounter As Integer

'****************************************
' Create Player String Variables
'****************************************

Dim Player1 As String
Dim Player2 As String

'****************************************
' Create Team/GameSequence Variables based on Number of Teams
'****************************************
Dim Team(50) As String
Dim GameSequence(50) As String
Dim TeamNames(1 To 50) As String

Set cnn = CurrentProject.Connection
Set rstTeams = New ADODB.Recordset
Set rstFixtures = New ADODB.Recordset



    '*********************************************************
    'Open the Tables Teams and Fixtures
    '*********************************************************
    rstTeams.Open "SELECT * FROM tblTeams Where leagueno = " & intLeagueno & "", cnn, adOpenKeyset, adLockOptimistic
    'Where AgeGroup = 'u" & Age & "'"
    
    rstFixtures.Open "tblFixtures", cnn, adOpenKeyset, adLockOptimistic
    
    '****************************************************
    ' Read the Team Names into an Array
    '****************************************************
    iCounter = 1
    
    Do While Not rstTeams.EOF

        TeamNames(iCounter) = rstTeams.Fields("Team")
        iCounter = iCounter + 1
        rstTeams.MoveNext
    
    Loop
    
    '*****************************
    'Set Main constants
    '*****************************
    NumberofTeams = iCounter - 1
    NumberofFixtures = NumberofTeams - 1
    NumberofMatches = NumberofTeams / 2
    
    '*****************************************************
    ' Clear the Game Sequence Array
    '*****************************************************
    For iCounter = 1 To NumberofFixtures
        GameSequence(iCounter) = ""
    Next iCounter
    
    '*****************************************************
    ' Clear the Teams Array
    '*****************************************************
    For iCounter = 1 To NumberofTeams
        Team(iCounter) = iCounter
    Next iCounter
    
    FirstTeam = 0
    
    '*****************************************************
    ' Create the Game Sequence ready for the fixtures
    '*****************************************************
    For Week = 1 To NumberofFixtures
        FirstTeam = FirstTeam + 1
        
        For iCounter = FirstTeam To FirstTeam + NumberofFixtures - 1
            If iCounter > (NumberofFixtures) Then
                LastTeam = iCounter - NumberofFixtures
            Else
                LastTeam = iCounter
            End If
            GameSequence(Week) = GameSequence(Week) & " " & Format(Team(LastTeam), "00")
        Next iCounter
        GameSequence(Week) = Trim(GameSequence(Week)) + " " & Format(Team(NumberofTeams), "00")
    Next Week
    
    '***************************************************
    'Insert the new fixtures into the Table
    '***************************************************
    For Week = 1 To NumberofFixtures
        StartPosition = 1
        'Debug.Print "Week " & Week
        For iCounter = 1 To NumberofMatches
            Player1 = Mid(GameSequence(Week), StartPosition, 2)
            Player2 = Left(Right(GameSequence(Week), (StartPosition) + 1), 2)
            StartPosition = StartPosition + 3
            
            rstFixtures.AddNew
            rstFixtures.Fields("WeekNo") = Week
            'rstFixtures.Fields("HomeTeam") = TeamNames(HomeTeam)
            rstFixtures.Fields("Player1") = TeamNames(Player1)
            'rstFixtures.Fields("AwayTeam") = TeamNames(AwayTeam)
            rstFixtures.Fields("Player2") = TeamNames(Player2)
            'rstFixtures.Fields("Age") = Age
            rstFixtures.Fields("FixDate") = startdate
            rstFixtures.Fields("Leagueno") = intLeagueno
            rstFixtures.Update
        
        Next iCounter
    startdate = startdate + 7
    If startdate > EndDate Then Week = NumberofFixtures + 1
    Next Week

'****************************************
'Close the tables
'****************************************
rstTeams.Close
Set rstTeams = Nothing
rstFixtures.Close
Set rstFixtures = Nothing

End Function

VBA Function Collection for converting Eastings and Northings to Latitude and Longitude

Some years back we hired a young lad by the name of Iain Brodie on a temporary contract – The week before I had been at an ESRI conference which had extensively discussed Web Mapping and  a speaker had demonstrated showing points in Google Maps. It was clear to me that the Google Maps url would accept and zoom to coordinates if those coordinates passed to it were Longitude and Latitude. Where I work there are significant numbers of datasets that use old Ordnance Survey UK specific Eastings and Northings coordinate system. Ordnance Survey actually set out the mathematics of conversion to Lat and Long on this page even detailing coded functions albeit in Javascript.

http://www.movable-type.co.uk/scripts/latlong-gridref.html

I specifically wanted to dynamically convert using Visual Basic for applications (specifically from MS Access). When Iain arrived it was clear that he was useful with computers and so I tasked him with finding VBA code from the internet. Between us we managed to get it working and I still regularly use the function set today to give users of applications a map in Google Maps. It really is a very nice quick tool that gives users quick access to maps for – you bet zero cost. My favourite price. We originally had it working with Google Earth but I only use it with Google Maps now.

Function PHId(North1, N0, aFo, PHI0, n, bFo)
PHI1 = ((North1 - N0) / aFo) + PHI0
M = Marc(bFo, n, PHI0, PHI1)
PHI2 = ((North1 - N0 - M) / aFo) + PHI1
Do While Abs(North1 - N0 - M) &gt; 0.00001
PHI2 = ((North1 - N0 - M) / aFo) + PHI1
M = Marc(bFo, n, PHI0, PHI2)
PHI1 = PHI2
Loop
PHId = PHI2
End Function

Function Marc(bFo, n, P1, P2)
Marc = bFo * (((1 + n + ((5 / 4) * (n ^ 2)) + ((5 / 4) * (n ^ 3))) * (P2 - P1)) - (((3 * n) + (3 * (n ^ 2)) + ((21 / 8) * (n ^ 3))) * (Sin(P2 - P1)) * (Cos(P2 + P1))) + ((((15 / 8) * (n ^ 2)) + ((15 / 8) * (n ^ 3))) * (Sin(2 * (P2 - P1))) * (Cos(2 * (P2 + P1)))) - (((35 / 24) * (n ^ 3)) * (Sin(3 * (P2 - P1))) * (Cos(3 * (P2 + P1)))))
End Function

Function lon(East1, North1)
a = 6377563.396
b = 6356256.91
F0 = 0.9996012717
E0 = 400000
N0 = -100000
PHI0 = 0.855211333
LAM0 = -0.034906585
aFo = a * F0
bFo = b * F0
e2 = (aFo ^ 2 - bFo ^ 2) / aFo ^ 2
n = (aFo - bFo) / (aFo + bFo)
InitPHI = PHId(North1, N0, aFo, PHI0, n, bFo)
nuPL = aFo / ((1 - (e2 * (Sin(InitPHI)) ^ 2)) ^ 0.5)
rhoPL = (nuPL * (1 - e2)) / (1 - (e2 * (Sin(InitPHI)) ^ 2))
eta2PL = (nuPL / rhoPL) - 1
M = Marc(bFo, n, PHI0, InitPHI)
Et = East1 - E0
X = ((Cos(InitPHI)) ^ -1) / nuPL
XI = (((Cos(InitPHI)) ^ -1) / (6 * nuPL ^ 3)) * ((nuPL / rhoPL) + (2 * ((Tan(InitPHI)) ^ 2)))
XII = (((Cos(InitPHI)) ^ -1) / (120 * nuPL ^ 5)) * (5 + (28 * ((Tan(InitPHI)) ^ 2)) + (24 * ((Tan(InitPHI)) ^ 4)))
XIIA = (((Cos(InitPHI)) ^ -1) / (5040 * nuPL ^ 7)) * (61 + (662 * ((Tan(InitPHI)) ^ 2)) + (1320 * ((Tan(InitPHI)) ^ 4)) + (720 * ((Tan(InitPHI)) ^ 6)))
lon = (LAM0 + (Et * X) - ((Et ^ 3) * XI) + ((Et ^ 5) * XII) - ((Et ^ 7) * XIIA))
End Function

Function lat(East1, North1)
a = 6377563.396
b = 6356256.91
F0 = 0.9996012717
E0 = 400000
N0 = -100000
PHI0 = 0.855211333
LAM0 = -0.034906585
aFo = a * F0
bFo = b * F0
e2 = (aFo ^ 2 - bFo ^ 2) / aFo ^ 2
n = (aFo - bFo) / (aFo + bFo)
InitPHI = PHId(North1, N0, aFo, PHI0, n, bFo)
nuPL = aFo / ((1 - (e2 * (Sin(InitPHI)) ^ 2)) ^ 0.5)
rhoPL = (nuPL * (1 - e2)) / (1 - (e2 * (Sin(InitPHI)) ^ 2))
eta2PL = (nuPL / rhoPL) - 1
M = Marc(bFo, n, PHI0, InitPHI)
Et = East1 - E0
VII = (Tan(InitPHI)) / (2 * nuPL * rhoPL)
VIII = ((Tan(InitPHI)) / (24 * rhoPL * nuPL ^ 3)) * (5 + (3 * ((Tan(InitPHI)) ^ 2)) + eta2PL - (9 * ((Tan(InitPHI)) ^ 2) * eta2PL))
IX = ((Tan(InitPHI)) / (720 * rhoPL * nuPL ^ 5)) * (61 + (90 * ((Tan(InitPHI)) ^ 2)) + (45 * ((Tan(InitPHI)) ^ 4)))
lat = (InitPHI - ((Et ^ 2) * VII) + ((Et ^ 4) * VIII) - ((Et ^ 6) * IX))
End Function

Function degrees(radians)
degrees = 180 * radians / 3.14159265358979
End Function

Function trunc(value)
If value &gt; 0 Then
trunc = Int(value)
Else
trunc = Int(value + 1)
End If
End Function

And here is the code the onclick function of a button called Command01 and it pulls from a screen that has an eastings and northings field on it and which has a Sitename field.

Dim Llatitude As Double
Dim Llongitude As Double
Dim strSitename As String

Llatitude = degrees(lat([Eastings], [Northings]))
Llongitude = degrees(lon([Eastings], [Northings])) - 0.0015
strSitename = Me.Sitename
    
Dim strlatlong As String
strlatlong = Llatitude & ",+" & Llongitude

‘Here I have two options – the first places a marker on the map – as far as I can tell – the marker is only available within google with the side panel displayed as well. The second shows the map centered on the requested location but without any markers. Choose one

Command01.HyperlinkAddress = "https://maps.google.com/maps?q=" & strlatlong & "+(" & strSitename & ")&z=18&iwloc=near&hl=en&ll=" & strlatlong

Command01.HyperlinkAddress ="https://www.google.com/maps/@" & Llatitude & "," & Llongitude & ",18z?hl=en"

And for Developers wanting to get into more detail here is the url for more information on passing parameters to the google maps url.

Google Map URLs